Greedy Algorithms

Hey Guys !!! Welcome back to the Algorithm shelf . Next type is all about Greedy Algorithm. You might be learn this type but I think your not able to remind it so lets create permanent access in your memory called “Mind”.

As we know the meaning of Greedy is nothing but the behavior of wanting more than you are entitled to. The algorithm is also same as the behavior it makes the choice for the best solution.

Basics:

Greedy Algorithm divides the problem in number of sub-problems ; then it will choose the best solution from all the solutions of sub-problems (Local Optimal , Greedy Choice) The hope : A locally optimal solution will lead to the globally optimal solution ; it might be work for some problems .

Reasons: Designed to achieve optimum solution for a given problem . As being greedy, the closest solution that seems to provide an optimal solution is chosen. It find the locally optimal solution which leads to the globally optimal solution , however greedy algorithm do not provide globally optimal solution directly.

Example to be solved : Greedy Algorithm always go for the networking problems like given below.

• Traveling Salesman Problem
• Prim’s Minimal Spanning Tree Algorithm
• Kruskal’s Minimal Spanning Tree Algorithm
• Dijkstra’s Minimal Spanning Tree Algorithm
• Graph – Map Coloring
• Graph – Vertex Cover
• Knapsack Problem
• Job Scheduling Problem

Traveling Salesman Problem : Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point. Note the difference between Hamiltonian Cycle and TSP. The Hamiltoninan cycle problem is to find if there exist a tour that visits every city exactly once. Here we know that Hamiltonian Tour exists (because the graph is complete) and in fact many such tours exist, the problem is to find a minimum weight Hamiltonian Cycle.

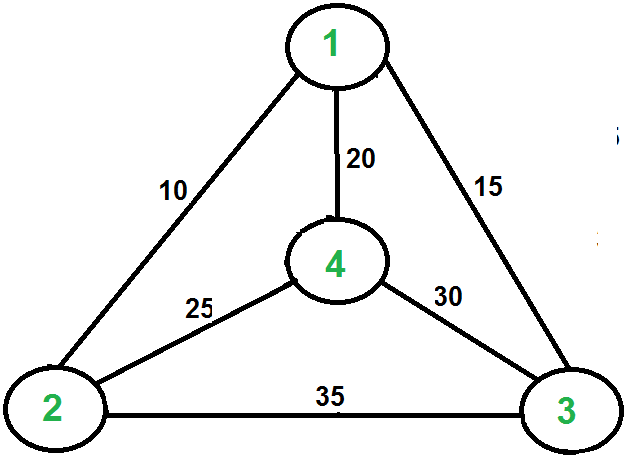
For example, consider the graph shown in figure on right side. A TSP tour in the graph is 1-2-4-3-1. The cost of the tour is 10+25+30+15 which is 80. by considering the lowest cost for the tour.

Code : ( Language C )

<code>

#include <stdio.h>
int matrix[25][25], visited_cities[10], limit, cost = 0;
 
int tsp(int c)
{
 int count, nearest_city = 999;
 int minimum = 999, temp;
 for(count = 0; count < limit; count++)
 {
 if((matrix[c][count] != 0) && (visited_cities[count] == 0))
 {
 if(matrix[c][count] < minimum)
 {
 minimum = matrix[count][0] + matrix[c][count];
 }
 temp = matrix[c][count];
 nearest_city = count;
 }
 }
 if(minimum != 999)
 {
 cost = cost + temp;
 }
 return nearest_city;
}
 
void minimum_cost(int city)
{
 int nearest_city;
 visited_cities[city] = 1;
 printf("%d ", city + 1);
 nearest_city = tsp(city);
 if(nearest_city == 999)
 {
 nearest_city = 0;
 printf("%d", nearest_city + 1);
 cost = cost + matrix[city][nearest_city];
 return;
 }
 minimum_cost(nearest_city);
}
 
int main()
{ 
 int i, j;
 printf("Enter Total Number of Cities:\t");
 scanf("%d", &limit);
 printf("\nEnter Cost Matrix\n");
 for(i = 0; i < limit; i++)
 {
 printf("\nEnter %d Elements in Row[%d]\n", limit, i + 1);
 for(j = 0; j < limit; j++)
 {
 scanf("%d", &matrix[i][j]);
 }
 visited_cities[i] = 0;
 }
 printf("\nEntered Cost Matrix\n");
 for(i = 0; i < limit; i++)
 {
 printf("\n");
 for(j = 0; j < limit; j++)
 {
 printf("%d ", matrix[i][j]);
 }
 }
 printf("\n\nPath:\t");
 minimum_cost(0);
 printf("\n\nMinimum Cost: \t");
 printf("%d\n", cost);
 return 0;
}

</code>

Output :

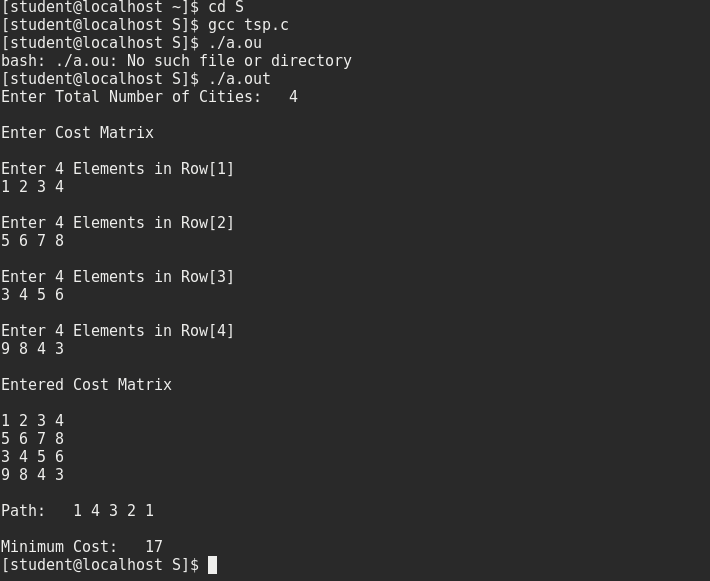
Hope this example is very simple to get the concept clear, Till then stay tuned stay connected to know about the next type. I’ll come back with next blog .